1. 개요

이 예제에서는 모서리 가중치 그래프의 최소 스패닝 트리(MST)를 찾기 위한 Boruvka 알고리즘의 Java 구현을 살펴보겠습니다 .

Prim 과 Kruskal의 알고리즘 보다 앞서 지만 여전히 둘 사이의 교차로 간주될 수 있습니다.

2. 보루브카의 알고리즘

바로 알고리즘으로 넘어가겠습니다. 약간의 역사와 알고리즘 자체를 살펴보겠습니다.

2.1. 역사

주어진 그래프의 MST를 찾는 방법 은 1926년 Otakar Boruvka 에 의해 처음 공식화되었습니다 . 이것은 컴퓨터가 존재하기도 훨씬 이전의 일이었고 실제로 효율적인 배전 시스템을 설계하기 위해 모델링되었습니다.

Georges Sollin은 1965년 이를 재발견하여 병렬 컴퓨팅에 사용했습니다.

2.2. 알고리즘

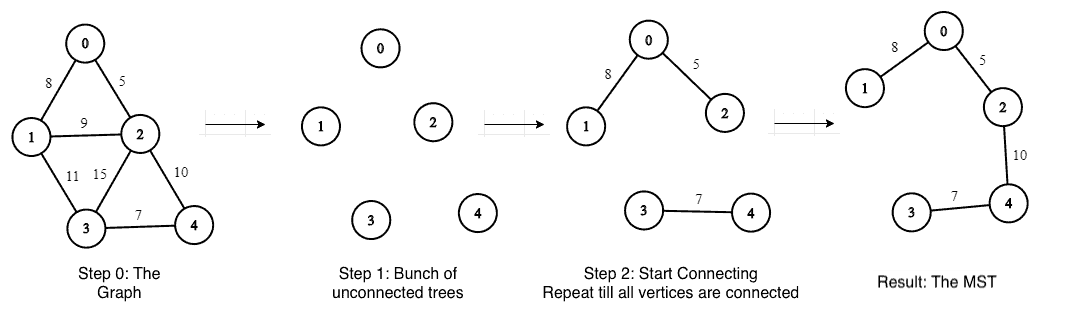
알고리즘의 핵심 아이디어는 각 정점이 고립된 나무를 나타내는 많은 나무로 시작하는 것입니다. 그런 다음 하나의 연결된 트리가 될 때까지 고립된 트리의 수를 줄이기 위해 가장자리를 계속 추가해야 합니다.

예시 그래프를 통해 이를 단계별로 살펴보겠습니다.

  • 0단계: 그래프 생성
  • 1단계: 연결되지 않은 트리로 시작합니다(트리 수 = 정점 수).
  • 2단계: 연결되지 않은 트리가 있는 동안 연결되지 않은 각 트리에 대해:
    • 더 가벼운 무게로 가장자리를 찾으십시오.
    • 이 가장자리를 추가하여 다른 나무를 연결합니다.

3. 자바 구현

이제 Java에서 이것을 구현하는 방법을 살펴보겠습니다.

3.1. UnionFind 데이터 구조

먼저 정점의 부모와 순위를 저장할 데이터 구조가 필요합니다 .

이 목적을 위해 union 과 find 의 두 가지 메서드를 사용하여 UnionFind 클래스를 정의해 보겠습니다 .

public class UnionFind {
    private int[] parents;
    private int[] ranks;

    public UnionFind(int n) {
        parents = new int[n];
        ranks = new int[n];
        for (int i = 0; i < n; i++) {
            parents[i] = i;
            ranks[i] = 0;
        }
    }

    public int find(int u) {
        while (u != parents[u]) {
            u = parents[u];
        }
        return u;
    }

    public void union(int u, int v) {
        int uParent = find(u);
        int vParent = find(v);
        if (uParent == vParent) {
            return;
        }

        if (ranks[uParent] < ranks[vParent]) { 
            parents[uParent] = vParent; 
        } else if (ranks[uParent] > ranks[vParent]) {
            parents[vParent] = uParent;
        } else {
            parents[vParent] = uParent;
            ranks[uParent]++;
        }
    }
}

우리는 이 클래스를 정점 간의 관계를 유지하고 점차적으로 MST를 구축하기 위한 도우미 구조로 생각할 수 있습니다.

확인하려면 여부를 두 정점 U 와 V를 경우 동일한 트리에 속해, 우리가 볼 찾기는 (유) 와 같은 부모를 반환 찾기 (V) . 노조 방법은 나무를 결합하는 데 사용됩니다. 이 사용법은 곧 보게 될 것입니다.

3.2. 사용자로부터 그래프 입력

이제 사용자로부터 그래프의 꼭짓점과 가장자리를 가져와서 런타임에 알고리즘에서 사용할 수 있는 개체에 매핑하는 방법이 필요합니다.

알고리즘을 테스트하기 위해 JUnit을 사용할 것이므로 이 부분은 @Before 메소드로 이동합니다.

@Before
public void setup() {
    graph = ValueGraphBuilder.undirected().build();
    graph.putEdgeValue(0, 1, 8);
    graph.putEdgeValue(0, 2, 5);
    graph.putEdgeValue(1, 2, 9);
    graph.putEdgeValue(1, 3, 11);
    graph.putEdgeValue(2, 3, 15);
    graph.putEdgeValue(2, 4, 10);
    graph.putEdgeValue(3, 4, 7);
}

여기서는 Guava의 MutableValueGraph<Integer, Integer> 를 사용하여 그래프를 저장했습니다. 그런 다음 ValueGraphBuilder 를 사용 하여 무방향 가중치 그래프를 구성했습니다.

방법 putEdgeValue는 세 개의 인수를 취 정수 의 정점에, 세 번째 정수 로 지정된, 그 무게를 MutableValueGraph 의 일반적인 유형 선언.

우리가 볼 수 있듯이 이것은 이전의 다이어그램에 표시된 것과 동일한 입력입니다.

3.3. 최소 스패닝 트리 도출

마지막으로 문제의 핵심인 알고리즘 구현에 도달했습니다.

BoruvkaMST 라고 하는 클래스에서 이 작업을 수행합니다 . 먼저 몇 가지 인스턴스 변수를 선언해 보겠습니다.

public class BoruvkaMST {
    private static MutableValueGraph<Integer, Integer> mst = ValueGraphBuilder.undirected().build();
    private static int totalWeight;
}

보시다시피 MST를 나타내기 위해 여기에서 MutableValueGraph<Integer, Integer>를 사용하고 있습니다.

둘째, 모든 마법이 일어나는 생성자를 정의합니다. 이전에 만든 그래프 라는 하나의 인수가 필요 합니다.

가장 먼저 하는 일은 입력 그래프 정점의 UnionFind 를 초기화하는 것 입니다. 처음에 모든 정점은 각각 순위가 0인 고유한 상위 정점입니다.

public BoruvkaMST(MutableValueGraph<Integer, Integer> graph) {
    int size = graph.nodes().size();
    UnionFind uf = new UnionFind(size);

다음으로, MST를 생성하는 데 필요한 반복 횟수를 정의하는 루프를 생성할 것입니다. 최대 log V번 또는 V-1 가장자리가 생길 때까지, 여기서 V는 정점의 수입니다.

for (int t = 1; t < size && mst.edges().size() < size - 1; t = t + t) {
    EndpointPair<Integer>[] closestEdgeArray = new EndpointPair[size];

여기서 우리는 또한 가장 가깝고 가중치가 낮은 가장자리를 저장하기 위해 가장자리 배열인 NearestEdgeArray를 초기화합니다 .

그런 다음, 그래프의 모든 가장자리를 반복하여 가장 가까운EdgeArray 를 채우는 내부 for 루프를 정의합니다 .

두 정점의 부모가 동일하면 동일한 트리이며 배열에 추가하지 않습니다. 그렇지 않으면 현재 모서리의 가중치를 상위 정점 모서리의 가중치와 비교합니다. 더 작으면 closeEdgeArray에 추가합니다 .

for (EndpointPair<Integer> edge : graph.edges()) {
    int u = edge.nodeU();
    int v = edge.nodeV();
    int uParent = uf.find(u);
    int vParent = uf.find(v);
    
    if (uParent == vParent) {
        continue;
    }

    int weight = graph.edgeValueOrDefault(u, v, 0);

    if (closestEdgeArray[uParent] == null) {
        closestEdgeArray[uParent] = edge;
    }
    if (closestEdgeArray[vParent] == null) {
        closestEdgeArray[vParent] = edge;
    }

    int uParentWeight = graph.edgeValueOrDefault(closestEdgeArray[uParent].nodeU(),
      closestEdgeArray[uParent].nodeV(), 0);
    int vParentWeight = graph.edgeValueOrDefault(closestEdgeArray[vParent].nodeU(),
      closestEdgeArray[vParent].nodeV(), 0);

    if (weight < uParentWeight) {
        closestEdgeArray[uParent] = edge;
    }
    if (weight < vParentWeight) {
        closestEdgeArray[vParent] = edge;
    }
}

그런 다음 두 번째 내부 루프를 정의하여 트리를 만듭니다. 같은 가장자리를 두 번 추가하지 않고 위 단계의 가장자리를 이 트리에 추가합니다. 또한 새로 생성된 나무 정점 의 상위 및 순위를 파생하고 저장하기 위해 UnionFind 에서 합집합 을 수행합니다 .

for (int i = 0; i < size; i++) {
    EndpointPair<Integer> edge = closestEdgeArray[i];
    if (edge != null) {
        int u = edge.nodeU();
        int v = edge.nodeV();
        int weight = graph.edgeValueOrDefault(u, v, 0);
        if (uf.find(u) != uf.find(v)) {
            mst.putEdgeValue(u, v, weight);
            totalWeight += weight;
            uf.union(u, v);
        }
    }
}

이 단계를 최대 log V번 반복하거나 V-1 에지를 가질 때까지 결과 트리가 MST입니다.

4. 테스트

마지막으로 구현을 확인하기 위해 간단한 JUnit을 살펴보겠습니다.

@Test
public void givenInputGraph_whenBoruvkaPerformed_thenMinimumSpanningTree() {
   
    BoruvkaMST boruvkaMST = new BoruvkaMST(graph);
    MutableValueGraph<Integer, Integer> mst = boruvkaMST.getMST();

    assertEquals(30, boruvkaMST.getTotalWeight());
    assertEquals(4, mst.getEdgeCount());
}

보시다시피 가중치가 30이고 모서리가 4개인 MST를 얻었습니다 . 그림의 예와 같습니다 .

5. 결론

이 예제에서 우리는 Boruvka 알고리즘의 Java 구현을 보았습니다. 시간 복잡도는 O(E log V)이며, 여기서 E는 간선의 수이고 V는 정점의 수입니다 .

항상 그렇듯이 소스 코드는 GitHub에서 사용할 수 있습니다 .

Generic footer banner

Spring으로 API를 빌드하는 방법을 배우 십니까?
전자책 다운로드