1. 소개
이 기사에서는 두 개의 정렬된 배열의 합집합에서 k 번째로 작은 요소 를 찾는 방법을 살펴보겠습니다 .
먼저 정확한 문제를 정의하겠습니다. 둘째, 두 가지 비효율적이지만 간단한 솔루션을 볼 수 있습니다. 셋째, 두 배열에 대한 이진 검색을 기반으로 하는 효율적인 솔루션을 살펴보겠습니다. 마지막으로 알고리즘이 작동하는지 확인하기 위해 몇 가지 테스트를 살펴보겠습니다.
알고리즘의 모든 부분에 대한 Java 코드 스니펫도 볼 수 있습니다. 단순화를 위해 구현은 정수에서만 작동합니다 . 그러나 설명된 알고리즘은 비교 가능하고 Generics를 사용하여 구현할 수도 있는 모든 데이터 유형에서 작동합니다.
2. 두 개의 정렬된 배열의 합집합에서 K 번째로 작은 요소 는 무엇입니까 ?
2.1. K 번째 작은 요소
찾기 위해 K TH-작은 소자도 불리는 K 배열 번째 차 통계치를, 우리는 일반적으로 사용하는 선택 알고리즘 . 그러나 이러한 알고리즘은 정렬되지 않은 단일 배열에서 작동하는 반면 이 기사에서는 두 개의 정렬된 배열에서 k 번째로 작은 요소 를 찾고자 합니다 .
문제에 대한 몇 가지 솔루션을 보기 전에 달성하고자 하는 바를 정확히 정의해 보겠습니다. 이를 위해 바로 예제로 넘어가겠습니다.
우리는 두 개의 배열 (분류 주어진 와 B 반드시 요소의 동일한 번호가 필요하지 않습니다) :
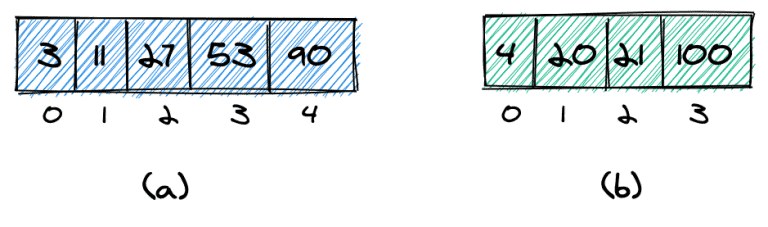
이 두 배열에서 k 번째로 작은 요소 를 찾고 싶습니다 . 더 구체적으로, 우리 는 결합되고 정렬된 배열에서 k 번째로 작은 요소 를 찾고 싶습니다 .

우리의 예를 위한 결합되고 정렬된 배열은 (c)에 나와 있습니다. 첫 번째로 작은 요소는 3 이고 네 번째로 작은 요소는 20 입니다.
2.2. 중복 값
또한 중복 값을 처리하는 방법을 정의해야 합니다. 요소는 배열 중 하나( 배열 a의 요소 3) 에서 두 번 이상 발생할 수 있으며 두 번째 배열( b ) 에서도 다시 발생할 수 있습니다 .
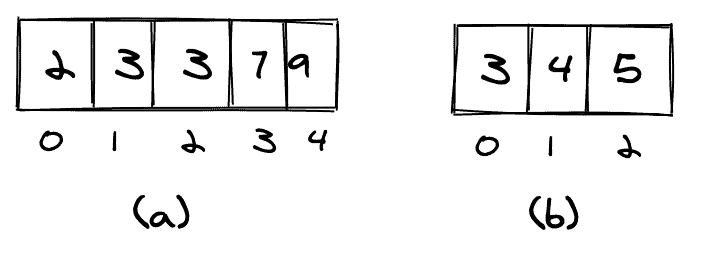
중복을 한 번만 계산하면 (c)와 같이 계산됩니다. 요소의 모든 발생을 계산하면 (d)와 같이 계산됩니다.
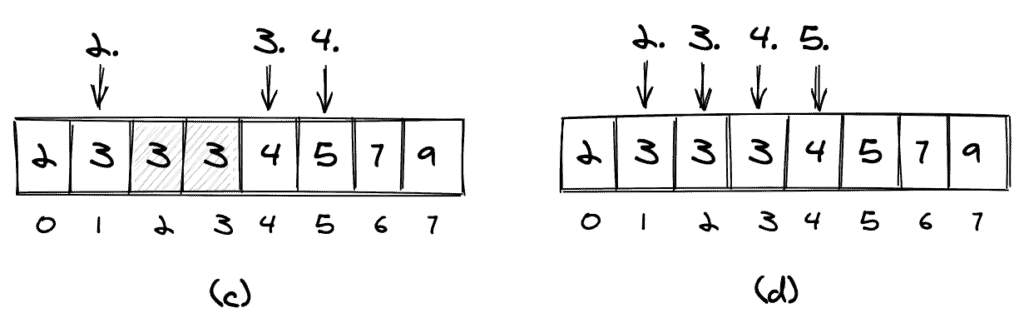
이 기사의 나머지 부분에서는 (d)와 같이 중복을 계산하여 별개의 요소인 것처럼 계산합니다.
3. 두 가지 간단하지만 덜 효율적인 접근 방식
3.1. 두 배열을 결합한 다음 정렬하기
k 번째로 작은 요소 를 찾는 가장 간단한 방법 은 배열을 결합하고 정렬 한 다음 결과 배열 의 k 번째 요소를 반환하는 것입니다 .
int getKthElementSorted(int[] list1, int[] list2, int k) {
int length1 = list1.length, length2 = list2.length;
int[] combinedArray = new int[length1 + length2];
System.arraycopy(list1, 0, combinedArray, 0, list1.length);
System.arraycopy(list2, 0, combinedArray, list1.length, list2.length);
Arrays.sort(combinedArray);
return combinedArray[k-1];
}함께 n 개의 제 배열의 길이 인 상기 제 2 어레이의 길이를 M, 우리는 결합 길이 얻을 N + m = C를 .
정렬의 복잡성이 O(c log c) 이므로 이 접근 방식의 전체 복잡성은 O(n log n) 입니다.
이 접근 방식의 단점은 어레이의 복사본을 생성해야 하므로 더 많은 공간이 필요하다는 것입니다.
3.2. 두 배열 병합
병합 정렬 정렬 알고리즘 의 단일 단계와 유사하게 두 배열을 병합 한 다음 k 번째 요소 를 직접 검색 할 수 있습니다 .
병합 알고리즘의 기본 아이디어는 첫 번째 및 두 번째 배열(a)의 첫 번째 요소를 가리키는 두 개의 포인터로 시작하는 것입니다.
그런 다음 포인터에서 두 요소( 3 및 4 ) 를 비교하고 더 작은 요소( 3 )를 결과에 추가하고 해당 포인터를 한 위치 앞으로(b) 이동합니다. 다시 포인터의 요소를 비교하고 더 작은 요소( 4 )를 결과에 추가합니다 .
결과 배열에 모든 요소가 추가될 때까지 같은 방식으로 계속합니다. 입력 배열 중 하나에 더 많은 요소가 없으면 다른 입력 배열의 나머지 요소를 모두 결과 배열에 복사합니다.
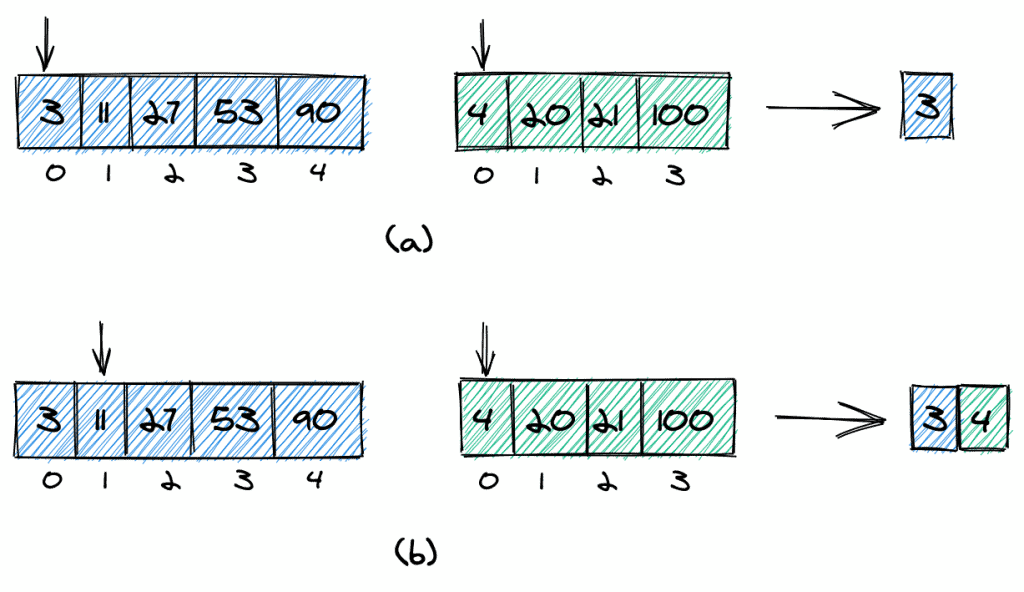
전체 배열을 복사하지 않으면 성능을 향상시킬 수 있지만 결과 배열에 k개의 요소 가 있으면 중지 합니다. 결합된 어레이에 대해 추가 어레이를 생성할 필요도 없지만 원래 어레이에서만 작동할 수 있습니다.
다음은 Java로 구현한 것입니다.
public static int getKthElementMerge(int[] list1, int[] list2, int k) {
int i1 = 0, i2 = 0;
while(i1 < list1.length && i2 < list2.length && (i1 + i2) < k) {
if(list1[i1] < list2[i2]) {
i1++;
} else {
i2++;
}
}
if((i1 + i2) < k) {
return i1 < list1.length ? list1[k - i2 - 1] : list2[k - i1 - 1];
} else if(i1 > 0 && i2 > 0) {
return Math.max(list1[i1-1], list2[i2-1]);
} else {
return i1 == 0 ? list2[i2-1] : list1[i1-1];
}
}이 알고리즘의 시간 복잡도가 O( k ) 임을 이해하는 것은 간단합니다 . 이 알고리즘의 장점은 중복 요소를 한 번만 고려하도록 쉽게 조정할 수 있다는 것 입니다.
4. 두 배열에 대한 이진 검색
O( k ) 보다 더 잘할 수 있습니까 ? 대답은 우리가 할 수 있다는 것입니다. 기본 아이디어는 두 배열에 대해 이진 검색 알고리즘을 수행하는 것입니다 .
이것이 작동하려면 모든 요소에 대한 지속적인 읽기 액세스를 제공하는 데이터 구조가 필요합니다. Java에서는 배열 또는 ArrayList 가 될 수 있습니다 .
구현하려는 메서드의 골격을 정의해 보겠습니다.
int findKthElement(int k, int[] list1, int[] list2)
throws NoSuchElementException, IllegalArgumentException {
// check input (see below)
// handle special cases (see below)
// binary search (see below)
}여기에서 k 와 두 개의 배열을 인수로 전달합니다. 먼저 입력의 유효성을 검사합니다. 둘째, 몇 가지 특별한 경우를 처리한 다음 이진 검색을 수행합니다. 다음 세 섹션에서는 이 세 단계를 역순으로 살펴볼 것이므로 먼저 이진 검색, 두 번째, 특수한 경우, 마지막으로 매개변수 유효성 검사를 살펴보겠습니다.
4.1. 이진 검색
특정 요소를 찾는 표준 이진 검색에는 두 가지 가능한 결과가 있습니다. 찾고 있는 요소를 찾고 검색에 성공하거나, 찾지 못해 검색에 실패하는 것입니다. 이것은 k 번째로 작은 요소 를 찾고자 하는 우리의 경우와 다릅니다 . 여기에서는 항상 결과가 있습니다.
이를 구현하는 방법을 살펴보겠습니다.
4.1.1. 두 배열에서 올바른 수의 요소 찾기
첫 번째 배열에서 특정 수의 요소로 검색을 시작합니다. 그 숫자를 nElementsList1 이라고 합시다 . 총 k개의 요소 가 필요하므로 nElementsList1 의 수 는 다음과 같습니다.
int nElementsList2 = k - nElementsList1;
예를 들어 k = 8 이라고 합시다 . 첫 번째 배열의 4개 요소와 두 번째 배열(a)의 4개 요소로 시작합니다.
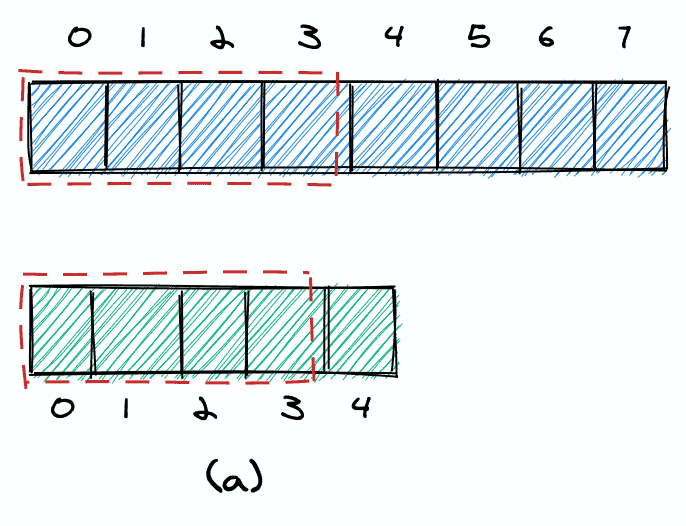
첫 번째 배열의 네 번째 요소가 두 번째 배열의 네 번째 요소보다 크면 첫 번째 배열에서 너무 많은 요소를 가져 와서 nElementsList1 (b)을 줄일 수 있음을 알 수 있습니다 . 그렇지 않으면 요소를 너무 적게 사용하여 nElementsList1 (b')을 늘릴 수 있다는 것을 알고 있습니다 .
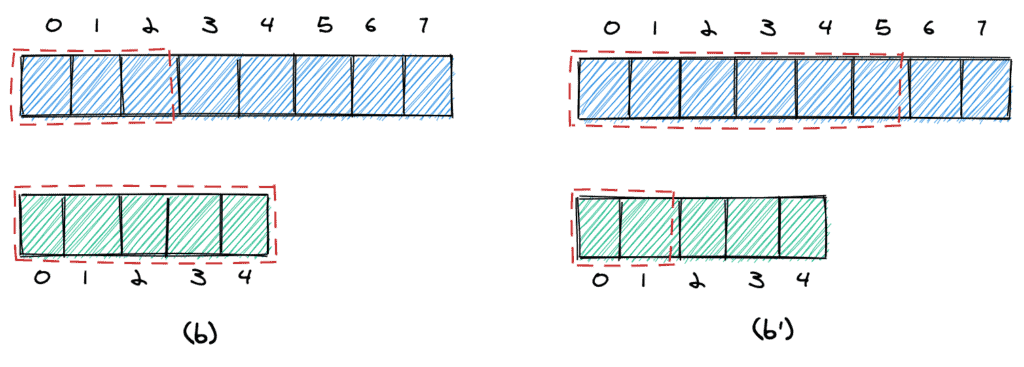
정지 기준에 도달할 때까지 계속합니다. 그것이 무엇인지 살펴보기 전에 지금까지 설명한 코드를 살펴보겠습니다.
int right = k;
int left = = 0;
do {
nElementsList1 = ((left + right) / 2) + 1;
nElementsList2 = k - nElementsList1;
if(nElementsList2 > 0) {
if (list1[nElementsList1 - 1] > list2[nElementsList2 - 1]) {
right = nElementsList1 - 2;
} else {
left = nElementsList1;
}
}
} while(!kthSmallesElementFound(list1, list2, nElementsList1, nElementsList2));4.1.2. 정지 기준
우리는 두 가지 경우에 멈출 수 있습니다. 첫째, 첫 번째 배열에서 가져온 최대 요소가 두 번째(c)에서 가져온 최대 요소와 같으면 중지할 수 있습니다. 이 경우 해당 요소를 간단히 반환할 수 있습니다.
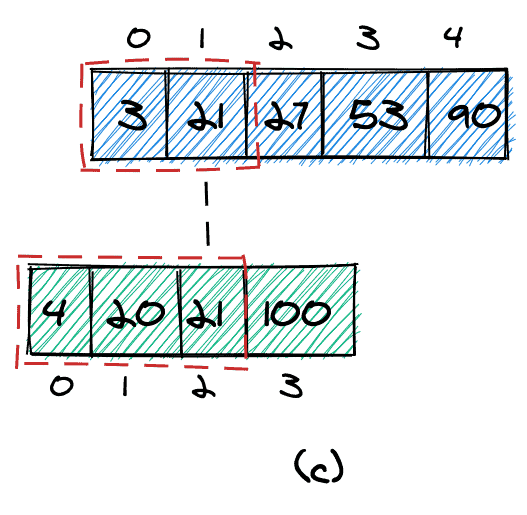
둘째, 다음 두 가지 조건(d)이 충족되면 중지할 수 있습니다.
- 첫 번째 배열에서 가져오는 가장 큰 요소는 두 번째 배열에서 가져오지 않은 가장 작은 요소보다 작습니다( 11 < 100 ).
- 두 번째 배열에서 가져오는 가장 큰 요소는 첫 번째 배열에서 가져오지 않은 가장 작은 요소보다 작습니다( 21 < 27 ).
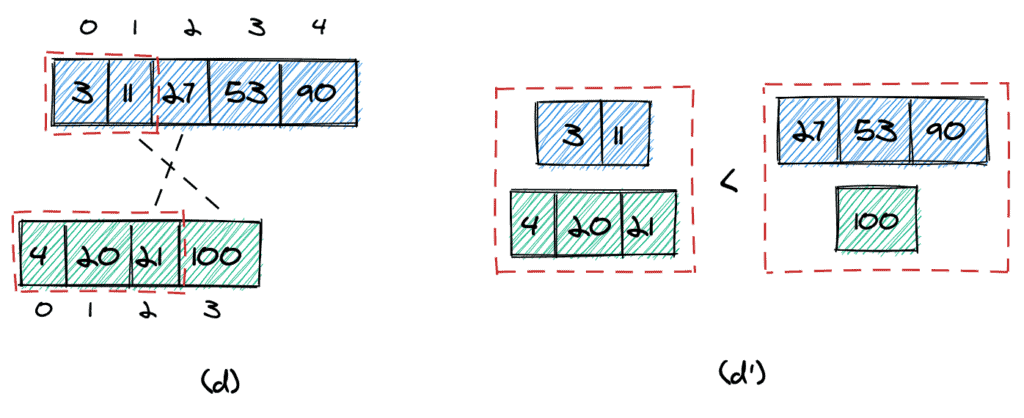
그 조건이 작동하는 이유(d')를 시각화하는 것은 쉽습니다. 두 배열에서 가져온 모든 요소는 두 배열의 다른 요소보다 확실히 작습니다.
중지 기준에 대한 코드는 다음과 같습니다.
private static boolean foundCorrectNumberOfElementsInBothLists(int[] list1, int[] list2, int nElementsList1, int nElementsList2) {
// we do not take any element from the second list
if(nElementsList2 < 1) {
return true;
}
if(list1[nElementsList1-1] == list2[nElementsList2-1]) {
return true;
}
if(nElementsList1 == list1.length) {
return list1[nElementsList1-1] <= list2[nElementsList2];
}
if(nElementsList2 == list2.length) {
return list2[nElementsList2-1] <= list1[nElementsList1];
}
return list1[nElementsList1-1] <= list2[nElementsList2] && list2[nElementsList2-1] <= list1[nElementsList1];
}4.1.3. 반환 값
마지막으로 올바른 값을 반환해야 합니다. 여기에 세 가지 가능한 경우가 있습니다.
- 두 번째 배열에서 요소를 가져오지 않으므로 대상 값은 첫 번째 배열(e)에 있습니다.
- 대상 값은 첫 번째 배열(e')에 있습니다.
- 대상 값은 두 번째 배열(e”)에 있습니다.
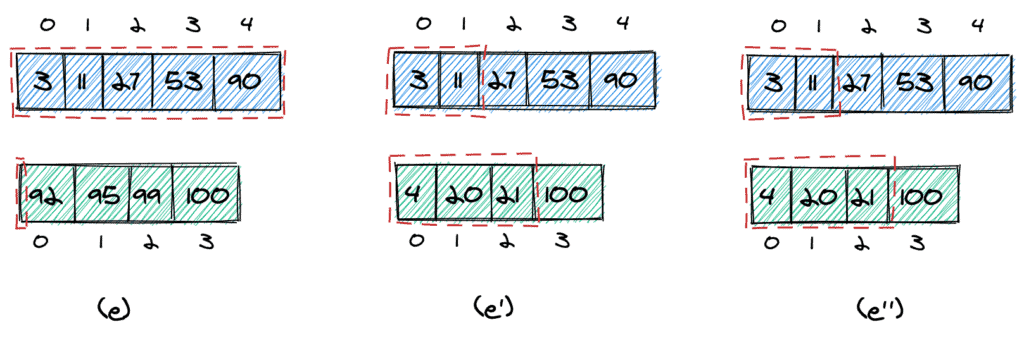
이것을 코드로 보자:
return nElementsList2 == 0 ? list1[nElementsList1-1] : max(list1[nElementsList1-1], list2[nElementsList2-1]);첫 번째 배열에서 요소를 가져오지 않는 경우를 처리할 필요가 없다는 점에 유의하십시오. 나중에 특별한 경우를 처리할 때 해당 경우를 제외합니다.
4.2. 왼쪽 및 오른쪽 테두리의 초기 값
지금까지 첫 번째 배열의 오른쪽 및 왼쪽 경계를 k 와 0 으로 초기화했습니다 .
int right = k;
int left = 0;그러나 k 값에 따라 이러한 경계를 조정해야 합니다.
먼저 k 가 첫 번째 배열의 길이를 초과하면 마지막 요소를 오른쪽 경계로 사용해야 합니다. 그 이유는 배열에서 더 많은 요소를 가져올 수 없기 때문에 매우 간단합니다.
둘째, k 가 두 번째 배열의 요소 수보다 크면 첫 번째 배열에서 최소한 (k – length(list2)) 를 가져와야 한다는 것을 압니다 . 예를 들어 k = 7 이라고 합시다 . 두 번째 배열에는 4개의 요소만 있으므로 첫 번째 배열 에서 최소 3 개의 요소를 가져와야 한다는 것을 알고 있으므로 L 을 2로 설정할 수 있습니다 .
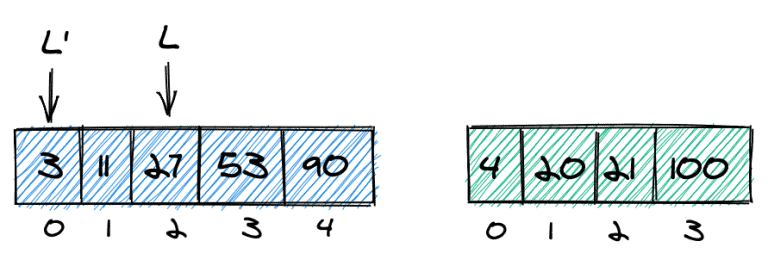
조정된 왼쪽 및 오른쪽 테두리에 대한 코드는 다음과 같습니다.
// correct left boundary if k is bigger than the size of list2
int left = k < list2.length ? 0 : k - list2.length - 1;
// the inital right boundary cannot exceed the list1
int right = min(k-1, list1.length - 1);4.3. 특별한 경우의 처리
실제 이진 검색을 수행하기 전에 알고리즘을 약간 덜 복잡하게 만들고 예외를 피하기 위해 몇 가지 특별한 경우를 처리할 수 있습니다. 어노테이션에 설명이 있는 코드는 다음과 같습니다.
// we are looking for the minimum value
if(k == 1) {
return min(list1[0], list2[0]);
}
// we are looking for the maximum value
if(list1.length + list2.length == k) {
return max(list1[list1.length-1], list2[list2.length-1]);
}
// swap lists if needed to make sure we take at least one element from list1
if(k <= list2.length && list2[k-1] < list1[0]) {
int[] list1_ = list1;
list1 = list2;
list2 = list1_;
}4.4. 입력 검증
먼저 입력 유효성 검사를 살펴보겠습니다. 예를 들어 NullPointerException 또는 ArrayIndexOutOfBoundsException 과 같은 알고리즘이 실패하고 throw되는 것을 방지하려면 세 개의 매개변수가 다음 조건을 충족하는지 확인해야 합니다.
- 두 배열 모두 null이 아니어야 하며 요소가 하나 이상 있어야 합니다.
- k 는 >= 0 이어야 하며 두 배열을 합한 길이보다 클 수 없습니다.
코드의 유효성 검사는 다음과 같습니다.
void checkInput(int k, int[] list1, int[] list2) throws NoSuchElementException, IllegalArgumentException {
if(list1 == null || list2 == null || k < 1) {
throw new IllegalArgumentException();
}
if(list1.length == 0 || list2.length == 0) {
throw new IllegalArgumentException();
}
if(k > list1.length + list2.length) {
throw new NoSuchElementException();
}
}4.5. 전체 코드
방금 설명한 알고리즘의 전체 코드는 다음과 같습니다.
public static int findKthElement(int k, int[] list1, int[] list2) throws NoSuchElementException, IllegalArgumentException {
checkInput(k, list1, list2);
// we are looking for the minimum value
if(k == 1) {
return min(list1[0], list2[0]);
}
// we are looking for the maximum value
if(list1.length + list2.length == k) {
return max(list1[list1.length-1], list2[list2.length-1]);
}
// swap lists if needed to make sure we take at least one element from list1
if(k <= list2.length && list2[k-1] < list1[0]) {
int[] list1_ = list1;
list1 = list2;
list2 = list1_;
}
// correct left boundary if k is bigger than the size of list2
int left = k < list2.length ? 0 : k - list2.length - 1;
// the inital right boundary cannot exceed the list1
int right = min(k-1, list1.length - 1);
int nElementsList1, nElementsList2;
// binary search
do {
nElementsList1 = ((left + right) / 2) + 1;
nElementsList2 = k - nElementsList1;
if(nElementsList2 > 0) {
if (list1[nElementsList1 - 1] > list2[nElementsList2 - 1]) {
right = nElementsList1 - 2;
} else {
left = nElementsList1;
}
}
} while(!kthSmallesElementFound(list1, list2, nElementsList1, nElementsList2));
return nElementsList2 == 0 ? list1[nElementsList1-1] : max(list1[nElementsList1-1], list2[nElementsList2-1]);
}
private static boolean foundCorrectNumberOfElementsInBothLists(int[] list1, int[] list2, int nElementsList1, int nElementsList2) {
// we do not take any element from the second list
if(nElementsList2 < 1) {
return true;
}
if(list1[nElementsList1-1] == list2[nElementsList2-1]) {
return true;
}
if(nElementsList1 == list1.length) {
return list1[nElementsList1-1] <= list2[nElementsList2];
}
if(nElementsList2 == list2.length) {
return list2[nElementsList2-1] <= list1[nElementsList1];
}
return list1[nElementsList1-1] <= list2[nElementsList2] && list2[nElementsList2-1] <= list1[nElementsList1];
}5. 알고리즘 테스트
GitHub 리포지토리에는 가능한 많은 입력 배열과 많은 코너 케이스를 다루는 많은 테스트 케이스가 있습니다.
여기에서는 정적 입력 배열에 대해 테스트하지 않고 이중 이진 검색 알고리즘의 결과를 간단한 결합 및 정렬 알고리즘의 결과와 비교하는 테스트 중 하나만 지적합니다. 입력은 두 개의 무작위 배열로 구성됩니다.
int[] sortedRandomIntArrayOfLength(int length) {
int[] intArray = new Random().ints(length).toArray();
Arrays.sort(intArray);
return intArray;
}다음 방법은 단일 테스트를 수행합니다.
private void random() {
Random random = new Random();
int length1 = (Math.abs(random.nextInt())) % 1000 + 1;
int length2 = (Math.abs(random.nextInt())) % 1000 + 1;
int[] list1 = sortedRandomIntArrayOfLength(length1);
int[] list2 = sortedRandomIntArrayOfLength(length2);
int k = (Math.abs(random.nextInt()) + 1) % (length1 + length2);
int result = findKthElement(k, list1, list2);
int result2 = getKthElementSorted(list1, list2, k);
int result3 = getKthElementMerge(list1, list2, k);
assertEquals(result2, result);
assertEquals(result2, result3);
}그리고 위의 메서드를 호출하여 다음과 같은 많은 테스트를 실행할 수 있습니다.
@Test
void randomTests() {
IntStream.range(1, 100000).forEach(i -> random());
}6. 결론
이 기사에서 우리는 정렬된 두 배열의 합집합에서 k 번째로 작은 요소 를 찾는 방법에 대한 여러 가지 방법을 보았습니다 . 먼저 간단하고 간단한 O(n log n) 알고리즘 을 보았고 , 그 다음에는 복잡도가 O(n) 인 버전을 , 마지막으로 O(log n) 에서 실행되는 알고리즘을 보았습니다 .
우리가 본 마지막 알고리즘은 훌륭한 이론적 연습입니다. 그러나 가장 실용적인 목적을 위해 처음 두 알고리즘 중 하나를 사용하는 것을 고려해야 합니다. 이 알고리즘은 두 배열에 대한 이진 검색보다 훨씬 간단합니다. 물론 성능이 문제라면 이진 검색이 해결책이 될 수 있습니다.
이 기사의 모든 코드는 GitHub에서 사용할 수 있습니다.

