1. 소개
길 찾기 알고리즘은 Map를 탐색하는 기술로 , 서로 다른 두 지점 사이의 경로를 찾을 수 있습니다. 서로 다른 알고리즘은 종종 알고리즘의 효율성과 알고리즘이 생성하는 경로의 효율성 측면에서 서로 다른 장단점을 가지고 있습니다.
2. 길찾기 알고리즘이란?
경로 찾기 알고리즘은 노드와 에지로 구성된 그래프를 그래프를 통한 경로로 변환하는 기술입니다 . 이 그래프는 트래버스가 필요한 모든 것이 될 수 있습니다. 이 기사에서는 런던 지하철 시스템의 일부를 횡단하려고 합니다.
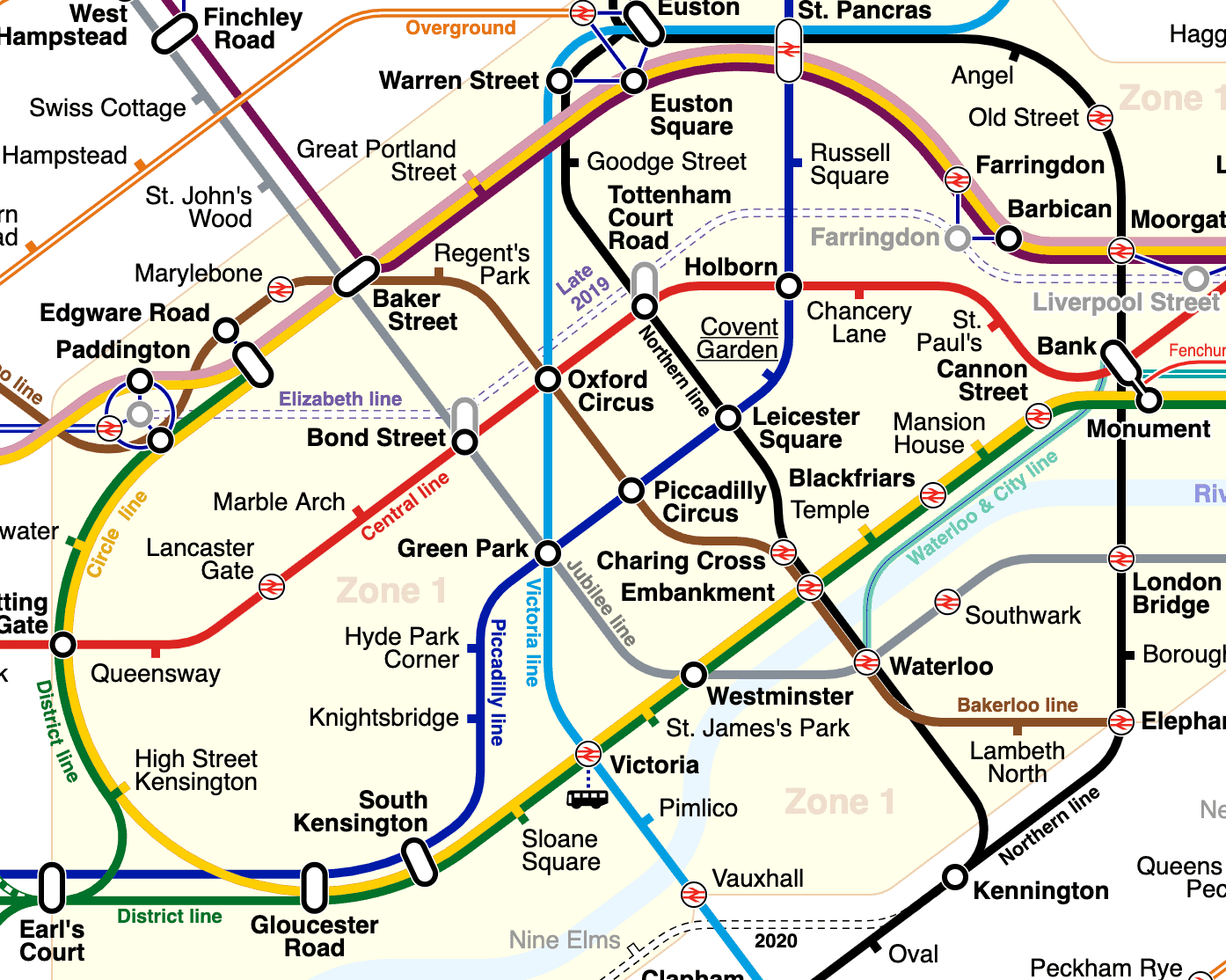
( sameboat 의 " London Underground Overground DLR Crossrail map " 은 CC BY-SA 4.0 에 따라 라이센스가 부여됩니다 . )
여기에는 많은 흥미로운 구성 요소가 있습니다.
- 출발점과 도착점 사이에 직접적인 경로가 있을 수도 있고 없을 수도 있습니다. 예를 들어 "Earl's Court"에서 "Monument"로 바로 이동할 수 있지만 "Angel"로는 갈 수 없습니다.
- 모든 단일 단계에는 특정 비용이 있습니다. 우리의 경우 이것은 역 사이의 거리입니다.
- 각 정류장은 다른 정류장의 작은 하위 집합에만 연결됩니다. 예를 들어 "Regent's Park"는 "Baker Street"와 "Oxford Circus"에만 직접 연결됩니다.
모든 경로 찾기 알고리즘은 모든 노드(우리의 경우 스테이션)와 이들 사이의 연결, 원하는 시작점과 Endpoints의 집합을 입력으로 사용합니다. 출력은 일반적으로 이동해야 하는 순서대로 처음부터 끝까지 우리를 데려다 줄 노드 집합입니다 .
3. A*란 무엇입니까?
A* 는 Peter Hart, Nils Nilsson 및 Bertram Raphael이 1968년에 처음 발표 한 특정 경로 찾기 알고리즘 중 하나 입니다. 일반적으로 경로를 미리 계산할 기회가 없고 메모리 사용에 대한 제약이 없을 때 사용하기에 가장 좋은 알고리즘으로 간주됩니다 .
메모리와 성능 복잡성 모두 최악의 경우 O(b^d) 가 될 수 있으므로 항상 가장 효율적인 경로를 찾아내지만 항상 가장 효율적인 방법은 아닙니다.
A*는 실제로 사용할 다음 노드를 선택하는 데 도움이 되는 추가 정보가 제공되는 Dijkstra's Algorithm의 변형입니다. 이 추가 정보가 완벽할 필요는 없습니다. 이미 완벽한 정보가 있다면 길 찾기는 무의미합니다. 그러나 더 좋을수록 최종 결과는 더 좋아질 것입니다.
4. A*는 어떻게 작동합니까?
A* 알고리즘은 지금까지 가장 좋은 경로를 반복적으로 선택하고 가장 좋은 다음 단계가 무엇인지 확인하는 방식으로 작동합니다.
이 알고리즘으로 작업할 때 추적해야 하는 몇 가지 데이터가 있습니다. "열린 세트"는 현재 고려 중인 모든 노드입니다. 이것은 시스템의 모든 노드가 아니라 다음 단계를 수행할 수 있는 모든 노드입니다.
또한 시스템의 각 노드에 대한 현재 최고 점수, 예상 총 점수 및 현재 최고 이전 노드를 추적합니다.
이것의 일부로 우리는 두 가지 다른 점수를 계산할 수 있어야 합니다. 하나는 한 노드에서 다음 노드로 가는 점수입니다. 두 번째는 모든 노드에서 대상까지의 비용 추정치를 제공하는 휴리스틱입니다. 이 추정치는 정확할 필요는 없지만 정확도가 높을수록 더 나은 결과를 얻을 수 있습니다. 유일한 요구 사항은 두 점수가 서로 일치해야 한다는 것입니다. 즉, 동일한 단위에 있어야 합니다.
맨 처음에 열린 세트는 시작 노드로 구성되며 다른 노드에 대한 정보는 전혀 없습니다.
반복할 때마다 다음을 수행합니다.
- 열린 세트에서 예상 총 점수가 가장 낮은 노드를 선택합니다.
- 열린 집합에서 이 노드를 제거합니다.
- 우리가 도달할 수 있는 모든 노드를 열린 집합에 추가합니다.
이 작업을 수행할 때 이 노드에서 각각의 새 점수로 새 점수를 계산하여 지금까지 얻은 것보다 개선되었는지 확인하고 개선된 경우 해당 노드에 대해 알고 있는 내용을 업데이트합니다.
그런 다음 예상 총 점수가 가장 낮은 개방형 세트의 노드가 목적지가 될 때까지 반복되며, 이 시점에서 경로를 갖게 됩니다.
4.1. 작업한 예
예를 들어 "Marylebone"에서 시작하여 "Bond Street"로 가는 길을 찾아봅시다.
맨 처음에 공개 세트는 "Marylebone"으로만 구성됩니다 . 즉, 이것이 암시적으로 최고의 "예상 총 점수"를 얻은 노드임을 의미합니다.
다음 정류장은 0.4403km의 "Edgware Road" 또는 0.4153km의 "Baker Street"입니다. 그러나 "Edgware Road"는 잘못된 방향에 있으므로 여기에서 목적지까지의 휴리스틱은 1.4284km의 점수를 제공하는 반면 "Baker Street"의 휴리스틱 점수는 1.0753km입니다.
이것은 이 반복 후에 우리의 열린 세트가 두 개의 항목으로 구성된다는 것을 의미합니다. 즉, 추정 총점 1.8687km의 "Edgware Road"와 추정 총점 1.4906km의 "Baker Street"입니다.
두 번째 반복은 "Baker Street"에서 시작할 것입니다. 왜냐하면 이것이 가장 낮은 예상 총 점수를 갖기 때문입니다. 여기에서 다음 정류장은 “Marylebone”, “St. John's Wood”, “Great Portland Street”, Regent's Park” 또는 “Bond Street”.
이 모든 것을 다루지는 않겠지만 "Marylebone"을 흥미로운 예로 들어보겠습니다. 거기에 도달하는 비용은 다시 0.4153km이지만 총 비용은 이제 0.8306km입니다. 또한 여기에서 목적지까지의 휴리스틱은 1.323km의 점수를 제공합니다.
즉, 예상 총 점수는 2.1536km 로 이 노드의 이전 점수보다 나쁩니다 . 이 경우 아무 것도 얻지 않으려면 추가 작업을 수행해야 했기 때문에 이것은 이치에 맞습니다. 이것은 우리가 이것을 실행 가능한 경로로 간주하지 않을 것임을 의미합니다. 따라서 "Marylebone"에 대한 세부 정보는 업데이트되지 않으며 공개 세트에 다시 추가되지 않습니다.
5. 자바 구현
이것이 어떻게 작동하는지 논의했으므로 이제 실제로 구현해 보겠습니다. 일반적인 솔루션을 구축한 다음 런던 지하철에서 작동하는 데 필요한 코드를 구현할 것입니다. 그런 다음 특정 부분만 구현하여 다른 시나리오에 사용할 수 있습니다.
5.1. 그래프 표현
첫째, 우리가 횡단하고자 하는 그래프를 표현할 수 있어야 합니다. 이것은 개별 노드와 전체 그래프의 두 가지 클래스로 구성됩니다.
GraphNode 라는 인터페이스를 사용하여 개별 노드를 나타냅니다 .
public interface GraphNode {
String getId();
}각 노드에는 ID가 있어야 합니다. 다른 것은 이 특정 그래프에만 해당되며 일반 솔루션에는 필요하지 않습니다. 이러한 클래스는 특별한 논리가 없는 단순한 Java Bean입니다.
전체 그래프는 간단히 Graph 라는 클래스로 표시됩니다 .
public class Graph<T extends GraphNode> {
private final Set<T> nodes;
private final Map<String, Set<String>> connections;
public T getNode(String id) {
return nodes.stream()
.filter(node -> node.getId().equals(id))
.findFirst()
.orElseThrow(() -> new IllegalArgumentException("No node found with ID"));
}
public Set<T> getConnections(T node) {
return connections.get(node.getId()).stream()
.map(this::getNode)
.collect(Collectors.toSet());
}
}이것은 그래프의 모든 노드를 저장하고 어떤 노드가 어떤 노드에 연결되는지 알고 있습니다. 그런 다음 ID로 노드를 가져오거나 지정된 노드에 연결된 모든 노드를 가져올 수 있습니다.
이 시점에서 우리는 원하는 수의 노드 사이에 있는 수의 가장자리를 사용하여 원하는 모든 형태의 그래프를 나타낼 수 있습니다.
5.2. 경로의 단계
다음으로 필요한 것은 그래프를 통해 경로를 찾는 메커니즘입니다.
첫 번째 부분은 두 노드 간에 점수를 생성하는 방법입니다. 다음 노드에 대한 점수와 목적지에 대한 추정치 모두에 대한 Scorer 인터페이스를 사용 합니다 .
public interface Scorer<T extends GraphNode> {
double computeCost(T from, T to);
}시작 노드와 끝 노드가 주어지면 노드 간 이동에 대한 점수를 얻습니다.
또한 추가 정보를 전달하는 노드 주위에 래퍼가 필요합니다. 이것은 GraphNode 가 아닌 RouteNode 입니다. 전체 그래프의 노드가 아니라 계산된 경로의 노드이기 때문입니다.
class RouteNode<T extends GraphNode> implements Comparable<RouteNode> {
private final T current;
private T previous;
private double routeScore;
private double estimatedScore;
RouteNode(T current) {
this(current, null, Double.POSITIVE_INFINITY, Double.POSITIVE_INFINITY);
}
RouteNode(T current, T previous, double routeScore, double estimatedScore) {
this.current = current;
this.previous = previous;
this.routeScore = routeScore;
this.estimatedScore = estimatedScore;
}
}GraphNode 와 마찬가지로 이들은 현재 경로 계산을 위해 각 노드의 현재 상태를 저장하는 데 사용되는 간단한 Java Bean입니다. 노드를 처음 방문하고 이에 대한 추가 정보가 아직 없는 일반적인 경우에 대해 간단한 생성자를 제공했습니다.
알고리즘의 일부로 예상 점수로 정렬할 수 있도록 비교 가능해야 합니다. 이는 Comparable 인터페이스 의 요구 사항을 충족하기 위해 compareTo() 메서드를 추가했음을 의미합니다.
@Override
public int compareTo(RouteNode other) {
if (this.estimatedScore > other.estimatedScore) {
return 1;
} else if (this.estimatedScore < other.estimatedScore) {
return -1;
} else {
return 0;
}
}5.3. 경로 찾기
이제 우리는 실제로 그래프에서 경로를 생성할 수 있는 위치에 있습니다. 이는 RouteFinder 라는 클래스가 됩니다 .
public class RouteFinder<T extends GraphNode> {
private final Graph<T> graph;
private final Scorer<T> nextNodeScorer;
private final Scorer<T> targetScorer;
public List<T> findRoute(T from, T to) {
throw new IllegalStateException("No route found");
}
}우리는 경로를 찾는 그래프와 다음 노드에 대한 정확한 점수에 대한 하나와 목적지까지의 예상 점수에 대한 두 개의 점수 기록기를 가지고 있습니다. 또한 시작 노드와 끝 노드를 가져와 둘 사이의 최적 경로를 계산하는 방법도 있습니다.
이 방법은 우리의 A* 알고리즘입니다. 나머지 코드는 모두 이 메서드 안에 들어갑니다.
몇 가지 기본 설정부터 시작합니다. 다음 단계로 고려할 수 있는 노드의 "개방형 세트"와 지금까지 방문한 모든 노드의 맵과 그에 대해 알고 있는 것입니다.
Queue<RouteNode> openSet = new PriorityQueue<>();
Map<T, RouteNode<T>> allNodes = new HashMap<>();
RouteNode<T> start = new RouteNode<>(from, null, 0d, targetScorer.computeCost(from, to));
openSet.add(start);
allNodes.put(from, start);우리의 열린 세트는 처음에 하나의 노드, 즉 시작점을 가집니다 . 이에 대한 이전 노드가 없고 거기에 도달하기 위한 점수가 0이며 목적지에서 얼마나 멀리 떨어져 있는지 추정할 수 있습니다.
열린 세트 에 PriorityQueue 를 사용 한다는 것은 이전의 compareTo() 메서드를 기반으로 자동으로 최상의 항목을 얻는다는 것을 의미합니다.
이제 살펴볼 노드가 부족하거나 사용 가능한 최상의 노드가 목적지가 될 때까지 반복합니다.
while (!openSet.isEmpty()) {
RouteNode<T> next = openSet.poll();
if (next.getCurrent().equals(to)) {
List<T> route = new ArrayList<>();
RouteNode<T> current = next;
do {
route.add(0, current.getCurrent());
current = allNodes.get(current.getPrevious());
} while (current != null);
return route;
}
// ...목적지를 찾으면 출발점에 도달할 때까지 이전 노드를 반복적으로 살펴Spring으로써 경로를 구축할 수 있습니다.
다음으로 목적지에 도달하지 못한 경우 다음에 수행할 작업을 알아낼 수 있습니다.
graph.getConnections(next.getCurrent()).forEach(connection -> {
RouteNode<T> nextNode = allNodes.getOrDefault(connection, new RouteNode<>(connection));
allNodes.put(connection, nextNode);
double newScore = next.getRouteScore() + nextNodeScorer.computeCost(next.getCurrent(), connection);
if (newScore < nextNode.getRouteScore()) {
nextNode.setPrevious(next.getCurrent());
nextNode.setRouteScore(newScore);
nextNode.setEstimatedScore(newScore + targetScorer.computeCost(connection, to));
openSet.add(nextNode);
}
});
throw new IllegalStateException("No route found");
}여기에서는 그래프에서 연결된 노드를 반복합니다. 이들 각각에 대해 우리가 가지고 있는 RouteNode 를 얻습니다. 필요한 경우 새 항목을 생성합니다.
그런 다음 이 노드에 대한 새 점수를 계산하고 지금까지 얻은 것보다 저렴한지 확인합니다. 그렇다면 이 새로운 경로와 일치하도록 업데이트하고 다음에 고려할 수 있도록 공개 세트에 추가합니다.
이것은 전체 알고리즘입니다. 우리는 목표에 도달하거나 도달하지 못할 때까지 이것을 계속 반복합니다.
5.4. 런던 지하철에 대한 구체적인 정보
지금까지 우리가 가지고 있는 것은 일반적인 A* 패스파인더 이지만 정확한 사용 사례에 필요한 세부 사항이 부족합니다. 즉, GraphNode 와 Scorer 모두의 구체적인 구현이 필요합니다 .
노드는 지하에 있는 스테이션이며 스테이션 클래스로 모델링합니다.
public class Station implements GraphNode {
private final String id;
private final String name;
private final double latitude;
private final double longitude;
}이름은 출력을 보는 데 유용하며 위도와 경도는 점수를 매기기 위한 것입니다.
이 시나리오에서는 Scorer 의 단일 구현만 필요합니다 . 이에 대해 Haversine 공식 을 사용하여 위도/경도의 두 쌍 사이의 직선 거리를 계산할 것입니다.
public class HaversineScorer implements Scorer<Station> {
@Override
public double computeCost(Station from, Station to) {
double R = 6372.8; // Earth's Radius, in kilometers
double dLat = Math.toRadians(to.getLatitude() - from.getLatitude());
double dLon = Math.toRadians(to.getLongitude() - from.getLongitude());
double lat1 = Math.toRadians(from.getLatitude());
double lat2 = Math.toRadians(to.getLatitude());
double a = Math.pow(Math.sin(dLat / 2),2)
+ Math.pow(Math.sin(dLon / 2),2) * Math.cos(lat1) * Math.cos(lat2);
double c = 2 * Math.asin(Math.sqrt(a));
return R * c;
}
}이제 두 쌍의 스테이션 사이의 경로를 계산하는 데 필요한 거의 모든 것이 있습니다. 빠진 유일한 것은 그들 사이의 연결 그래프입니다.
경로를 매핑하는 데 사용합시다. Earl's Court에서 Angel까지 하나를 생성합니다. 여기에는 최소 두 개의 튜브 라인에서 다양한 여행 옵션이 있습니다.
public void findRoute() {
List<Station> route = routeFinder.findRoute(underground.getNode("74"), underground.getNode("7"));
System.out.println(route.stream().map(Station::getName).collect(Collectors.toList()));
}이렇게 하면 Earl's Court -> South Kensington -> Green Park -> Euston -> Angel 경로가 생성됩니다.
많은 사람들이 선택했을 분명한 경로는 Earl's Count -> Monument -> Angel일 것입니다. 변경 사항이 적기 때문입니다. 대신, 이것은 더 많은 변화를 의미하지만 훨씬 더 직접적인 경로를 취했습니다.
6. 결론
이 기사에서 우리는 A* 알고리즘이 무엇인지, 어떻게 작동하는지, 우리 자신의 프로젝트에서 어떻게 구현하는지 살펴보았습니다. 이것을 가지고 당신 자신의 용도로 확장하지 않겠습니까?
튜브 라인 간의 교환을 고려하여 확장하고 선택한 경로에 어떤 영향을 미치는지 확인하십시오.
그리고 이 기사의 전체 코드는 GitHub에서 사용할 수 있습니다 .

